Linea Infinita de Carga
Campo eléctrico generado por una línea infinita de carga y densidad lineal de carga λ constante
La figura muestra una porción de una línea infinita de carga de densidad lineal de carga uniforme  .
.
 .
.La magnitud de la contribución de campo eléctrico  sobre el punto P debida al elemento de carga
sobre el punto P debida al elemento de carga  está dada por:
está dada por:
 sobre el punto P debida al elemento de carga
sobre el punto P debida al elemento de carga  está dada por:
está dada por: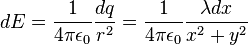 (1)
(1)El vector  tiene las componentes:
tiene las componentes:
 tiene las componentes:
tiene las componentes: y
y 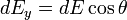
El signo menos delante de 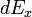 indica que
indica que 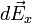 apunta en la dirección negativa de las x.
apunta en la dirección negativa de las x.
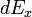 indica que
indica que 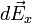 apunta en la dirección negativa de las x.
apunta en la dirección negativa de las x.Por tanto, las componentes x e y de  en el punto P, están dadas por:
en el punto P, están dadas por:
 en el punto P, están dadas por:
en el punto P, están dadas por:y
En estas expresiones 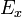 debe ser cero porque todo elemento de carga a la izquierda de la perpendicular que une P con la línea de carga tiene un elemento correspondiente a la derecha, de modo que sus contribuciones al campo en la dirección de las x se anulan mutuamente. Así pues,
debe ser cero porque todo elemento de carga a la izquierda de la perpendicular que une P con la línea de carga tiene un elemento correspondiente a la derecha, de modo que sus contribuciones al campo en la dirección de las x se anulan mutuamente. Así pues,  apunta exactamente en la dirección de las y. Como las contribuciones a
apunta exactamente en la dirección de las y. Como las contribuciones a  de la mitad derecha y de la mitad izquierda de la línea de carga son iguales, se puede escribir:
de la mitad derecha y de la mitad izquierda de la línea de carga son iguales, se puede escribir:
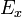 debe ser cero porque todo elemento de carga a la izquierda de la perpendicular que une P con la línea de carga tiene un elemento correspondiente a la derecha, de modo que sus contribuciones al campo en la dirección de las x se anulan mutuamente. Así pues,
debe ser cero porque todo elemento de carga a la izquierda de la perpendicular que une P con la línea de carga tiene un elemento correspondiente a la derecha, de modo que sus contribuciones al campo en la dirección de las x se anulan mutuamente. Así pues,  apunta exactamente en la dirección de las y. Como las contribuciones a
apunta exactamente en la dirección de las y. Como las contribuciones a  de la mitad derecha y de la mitad izquierda de la línea de carga son iguales, se puede escribir:
de la mitad derecha y de la mitad izquierda de la línea de carga son iguales, se puede escribir:
sustituyendo la expresión (1) en esta ecuación, se tiene:
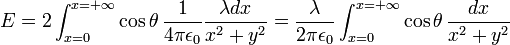 (2)
(2)Siendo 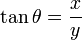 , se tiene
, se tiene  , diferenciando esta expresión resulta:
, diferenciando esta expresión resulta: 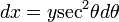 y sustituyendo en (2) se obtiene:
y sustituyendo en (2) se obtiene:
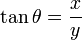 , se tiene
, se tiene  , diferenciando esta expresión resulta:
, diferenciando esta expresión resulta: 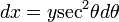 y sustituyendo en (2) se obtiene:
y sustituyendo en (2) se obtiene: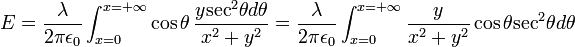 (3)
(3)Si se tiene en cuenta que:  ,
,  y
y  , se puede establecer que:
, se puede establecer que:
 ,
,  y
y  , se puede establecer que:
, se puede establecer que:
Sustituyendo en la expresión (3) se obtiene
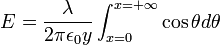
![E=\frac {\lambda }{2\pi {\epsilon}_0 y}\int_{\theta=0 }^{\theta =\frac {\pi }{2}} \cos \theta d \theta =\frac {\lambda }{2\pi {\epsilon}_0 y}\Bigg[ \sin \frac {\pi }{2}- \sin 0\Bigg] = \frac {\lambda }{2\pi {\epsilon}_0 y}](http://upload.wikimedia.org/math/0/4/7/047f2d16003ae41591da33454c20fcb4.png)
Por lo tanto:
 |
|---|
Extraído de la pagina Wikilibros. http://es.wikibooks.org/wiki/Electricidad/Campo_el%C3%A9ctrico/Campo_el%C3%A9ctrico_generado_por_una_distribuci%C3%B3n_continua_lineal_de_carga
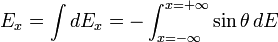

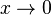
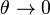
 ,
,  ,
,
0 comentarios: